
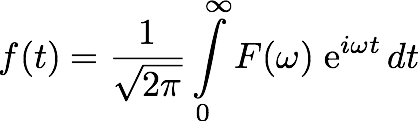
- Fourier transform equation for free#
- Fourier transform equation how to#
- Fourier transform equation series#

The time scale in the data is compressed by a factor of 10 to raise the pitch and make the call more clearly audible. Because blue whale calls are low-frequency sounds, they are barely audible to humans. Load and format a subset of the data in, which contains a Pacific blue whale vocalization.
This data can be found in a library maintained by the Cornell University Bioacoustics Research Program. Many specialized implementations of the fast Fourier transform algorithm are even more efficient when n is a power of 2.Ĭonsider audio data collected from underwater microphones off the coast of California. This computational efficiency is a big advantage when processing data that has millions of data points. DFT equation for the fundamental frequency (one.
Fourier transform equation series#
3.2 Fourier Series Consider a periodic function f f (x),dened on the interval 1 2 L x 1 2 L and having f (x + L) f (x)for all. Since the operation treats the data as if it were periodic, we evaluate the. To establish these results, let us begin to look at the details rst of Fourier series, and then of Fourier transforms.
Fourier transform equation how to#
If Mathematica knows how to solve the given initial value problem, you also have to know. The fast Fourier transform algorithm requires only on the order of n log n operations to compute. Fourier transforms take the process a step further, to a continuum of n-values. This gives us the solution: u(x, t) 1 2t e ( x ) 2 / ( 4t) f()d. $$ f(t) = \sum_ |\, x(n)|\, < \infty $$Īn absolutely summable sequence has always a finite energy but a finite-energy sequence is not necessarily to be absolutely summable.Using the Fourier transform formula directly to compute each of the n elements of y requires on the order of n 2 floating-point operations. One of the most useful properties of the Fourier transform is that it is its own inverse: if you apply a Fourier transform twice, you get the original function back. The complex Fourier series representation of f(t) is given as As mentioned before, the structure factor equation is a Fourier transform, which is a mathematical operation that has been studied for over a century. Deriving Fourier transform from Fourier seriesĬonsider a periodic signal f(t) with period T. Because it is not immediately obvious what S ( ) looks like for a given s ( t ), I have drawn a several Fourier transform pairs for comparison. That on the right is the inverse Fourier Transform. Remembering the fact that we introduced a factor of i (and including a factor of 2 that just crops up. The equation on the left is the Fourier Transform.
How about going back Recall our formula for the Fourier Series of f(t) : Now transform the sums to integrals from to, and again replace F m with F(). Compute answers using Wolframs breakthrough technology & knowledgebase, relied on by millions of students & professionals. The Fourier transform is defined for a vector x with n uniformly sampled points by. In signal processing, the Fourier transform can reveal important characteristics of a signal, namely, its frequency components.
Fourier transform equation for free#
where ( k) is eigenfunction of Schrodinger Equation for free particle. The Inverse Fourier Transform The Fourier Transform takes us from f(t) to F(). The Fourier transform is a mathematical formula that relates a signal sampled in time or space to the same signal sampled in frequency. i.e., ( x, t) 1 2 ( k) e i ( k x k 2 2 m t) d k. It is now time to look at a Fourier series. To overcome this shortcoming, Fourier developed a mathematical model to transform signals between time (or spatial) domain to frequency domain & vice versa, which is called 'Fourier transform'.įourier transform has many applications in physics and engineering such as analysis of LTI systems, RADAR, astronomy, signal processing etc. This means that we can write free particle with general wavefunction with ( x, t) as Fourier transform of eigenfunction of Schrodinger equation (I think). There are some naturally produced signals such as nonperiodic or aperiodic, which we cannot represent using Fourier series. The main drawback of Fourier series is, it is only applicable to periodic signals.


 0 kommentar(er)
0 kommentar(er)
